Welcome to PyLaplace!¶
PyLaplace is a Python implementation of generalized Laplace coefficients by three different methods. The generalized Laplace coefficients are defined by
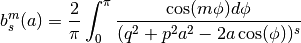
The result is determined by parameters  ,
,  ,
,
 ,
, 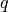 and
and 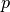 . These coefficients pop up
frequently in celestial mechanics and may need to be evaluated many
times, in which case brute force numerical integration is too
slow. Pylaplace includes two methods for faster evaluation, one based
on hypergeometric functions and an approximate method involving Bessel
functions.
. These coefficients pop up
frequently in celestial mechanics and may need to be evaluated many
times, in which case brute force numerical integration is too
slow. Pylaplace includes two methods for faster evaluation, one based
on hypergeometric functions and an approximate method involving Bessel
functions.
Installation¶
If Python is not installed, download from here and install. The latest versions of Python come with package manager pip included. Then PyLaplace can be installed from the command line simply by entering:
pip install pylaplace
Usage¶
Within Python, first import the class:
>>> from pylaplace import LaplaceCoefficient
Create an instance of LaplaceCoefficient:
>>> laplace = LaplaceCoefficient()
The generalized Laplace coefficient can then be calculated simply as:
>>> result = laplace(a, s, m, p, q)
The derivative with respect to  can be calculated using:
can be calculated using:
>>> result = laplace.derivative(a, s, m, p, q)
By default, the Laplace coefficients are calculated using hypergeometric functions. Two other methods are available: ‘Brute’ (brute force integration, very slow) and ‘Bessel’ (fast but approximate). These can be selected at creation by entering:
>>> laplace = LaplaceCoefficient(method='Brute')
Class reference¶
Class dealing with calculating generalized Laplace coefficients
Generalized Laplace coefficients can be calculated either by brute force integration (slow), hypergeometric functions (faster), or Bessel fuctions (fastest but approximate).
-
class
pylaplace.pylaplace.LaplaceCoefficient(method='Hyper')[source]¶ Class containing functions to calculate generalized Laplace coefficients.
The generalized Laplace coefficients are defined by
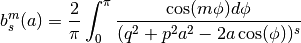
Parameters: method (str) – way to calculate the coefficients, either ‘Brute’ (brute force integration, slow but exact), ‘Hyper’ (hypergeometric functions, faster and exact), or ‘Bessel’ (Bessel functions, fastest but approximate) -
__call__(a, s, m, p, q)[source]¶ Calculate generalized Laplace coefficient.
Parameters: - a (float) – radius-like coordinate, must be smaller than unity
- s (float) – power to which denominator is raised
- m (float) – numerator of integrant is
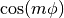
- p (float) – factor multiplying
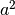 in denominator
in denominator - q (float) – constant term in denominator
-
derivative(a, s, m, p, q)[source]¶ Calculate derivative with respect to
 of generalized Laplace coefficient.
of generalized Laplace coefficient.Parameters: - a (float) – radius-like coordinate, must be smaller than unity
- s (float) – power to which denominator is raised
- m (float) – numerator of integrant is
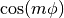
- p (float) – factor multiplying
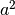 in denominator
in denominator - q (float) – constant term in denominator
-